数据结构（考试篇）

二叉树的先序遍历、后序遍历、中序遍历

先序遍历：根节点—>左节点–>右节点

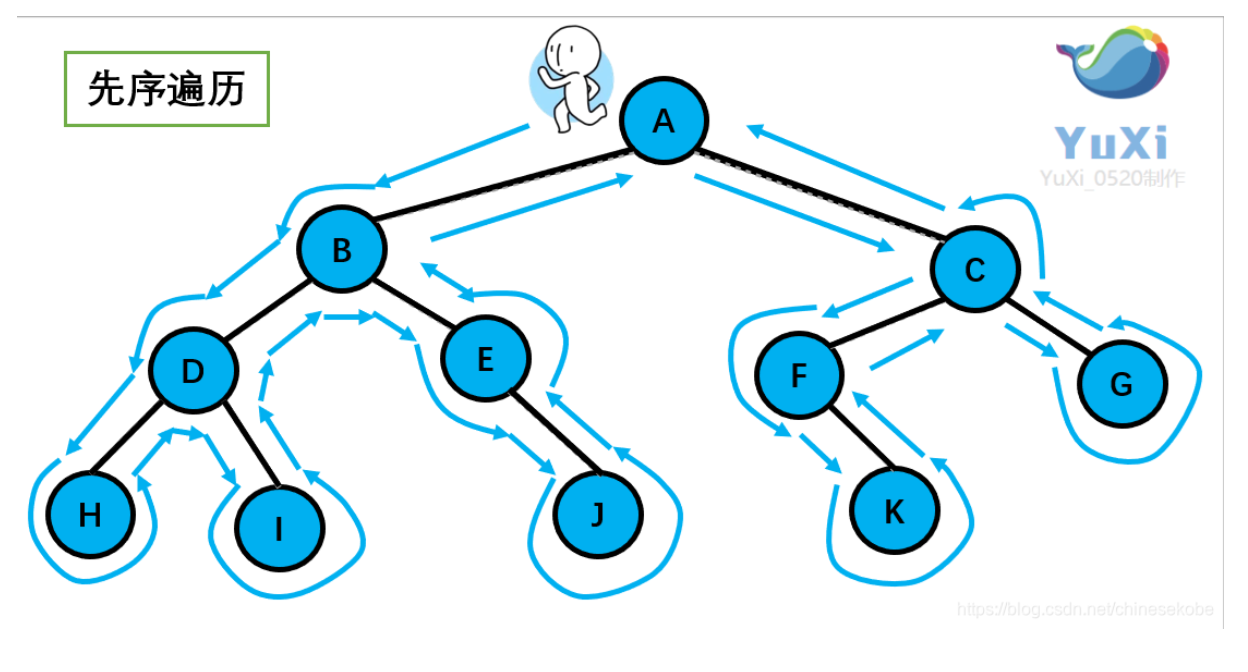
这个过程是递归的，比如说访问了左节点B之后不是去访问右节点C，而是去访问了以B为根节点的左节点D。顺序有个规律，可以看作是这个小人逆时针跑了一圈：A B D H I E J E C F K G

后序遍历：左节点–>右节点–>根节点

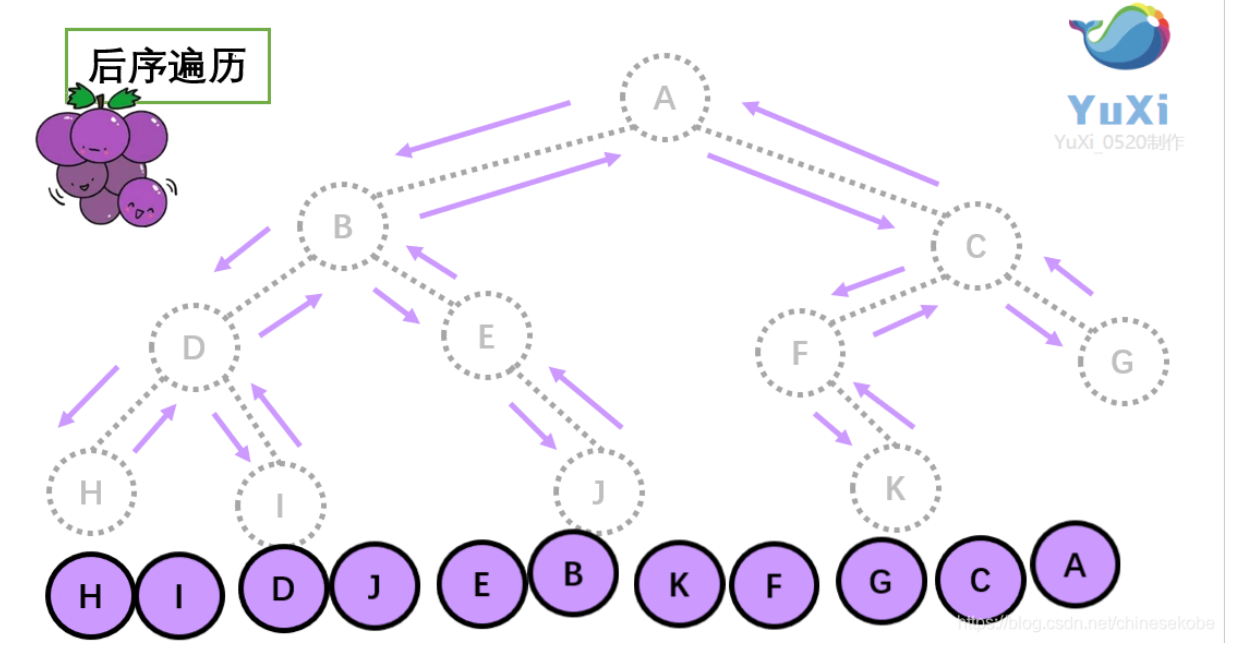
按照递归左右根就能排出来，排序小技巧是如图所示，当成一串葡萄，逆时针剪下最外面的一个单一葡萄。

中序遍历：左节点–>根节点–>右节点

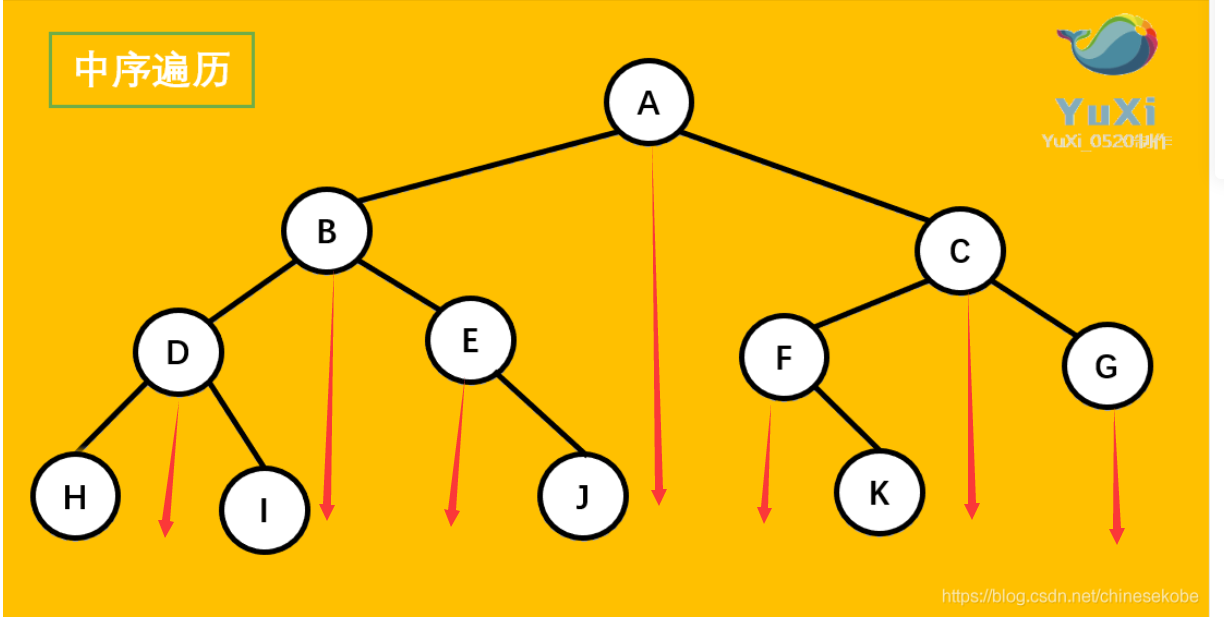
小技巧是看作竖直方向上的投影，其顺序是：HDIBEJAFKCG

参考：数据结构——二叉树先序、中序、后序及层次四种遍历（C语言版）_中序遍历-CSDN博客

度、节点计算

入度为0则为根节点，其余节点入度为1

出度则是子节点的个数，可取0、1、2。

总入度=节点总数-1，总入度=总出度

记节点出度为0、1、2的节点数分别为n0、n1、n2
则总出度N=n1+n2*2
总结点数=n0+n1+n2
根据 总入度=节点总数-1，总入度=总出度
则n0+n1+n2-1=n2*2+n1
所以n0=n2+1

一棵二叉树有十个度为2的节点，5个度为1的节点，求节点总数。10*2+5=n-1 n=25+1=26 26=15=11

节点总数等于度1+度2+度0，因此求出度为0的节点即可，即度2+1，所以10+1=11个。

参考：【精选】二叉树——度以及节点数的计算_二叉树节点和度的计算_不想做咸鱼的霉霉的博客-CSDN博客

计算时间复杂度

• 用常数1取代所有加法常数 O(199)—->O(1)
• 只保留最高阶O(n^2+n)—>O(n^2)
• 去除最高阶常数O(2*N^2)—->O(N^2)

O(2*N+10)—->O(N)

下面程序段的时间复杂度为（）。

i=1;

while(i<=n)

i=i*3;

(A) O(n)       (B) O(3n)

(C) O(log3n)   (D) O(n3)

正确答案是c，3^log3n=n。

存取结构

顺序存取和随机存取

随机存取（Random Access），指的是当存储器中的数据被读取或写入时，所需要的时间与该数据所在的物理地址无关，数组采用的就是随机存取，通过下标进行存取，存取arr[1]和存取arr[100]没有时间上的区别

顺序存取（Sequential access）是一种按记录的逻辑顺序进行读写操作的存取方法，所需的时间与数据所在的位置有关。

存储结构

顺序、链式、索引、哈希存储，后三个可以归为随机存储。

顺序存储：

相邻的数据存储在物理位置上相邻的存储单元。

优点：节省存储空间、可以实现随机存取

缺点：修改不方便、产生磁盘碎片

随机存储：

相邻的数据物理位置可以不相邻。

优点：不会产生磁盘碎片、修改数据方便

缺点：占用空间大、查找时比顺序存储慢，且只能实现顺序存取

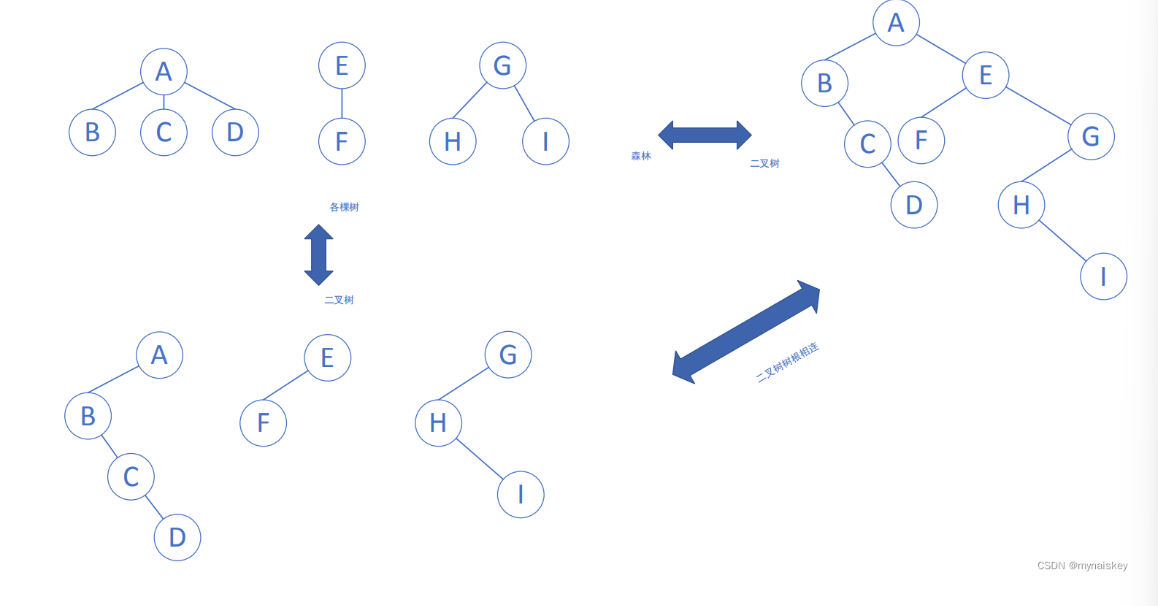
树和森林

树是一种非线性数据结构，树由唯一的根和若干互不相交的子树组成。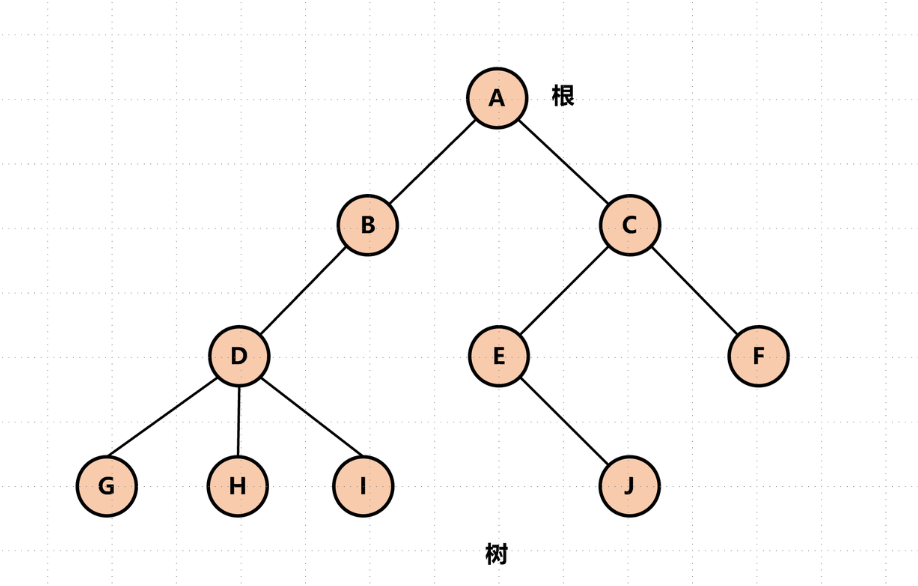

森林是树的集合。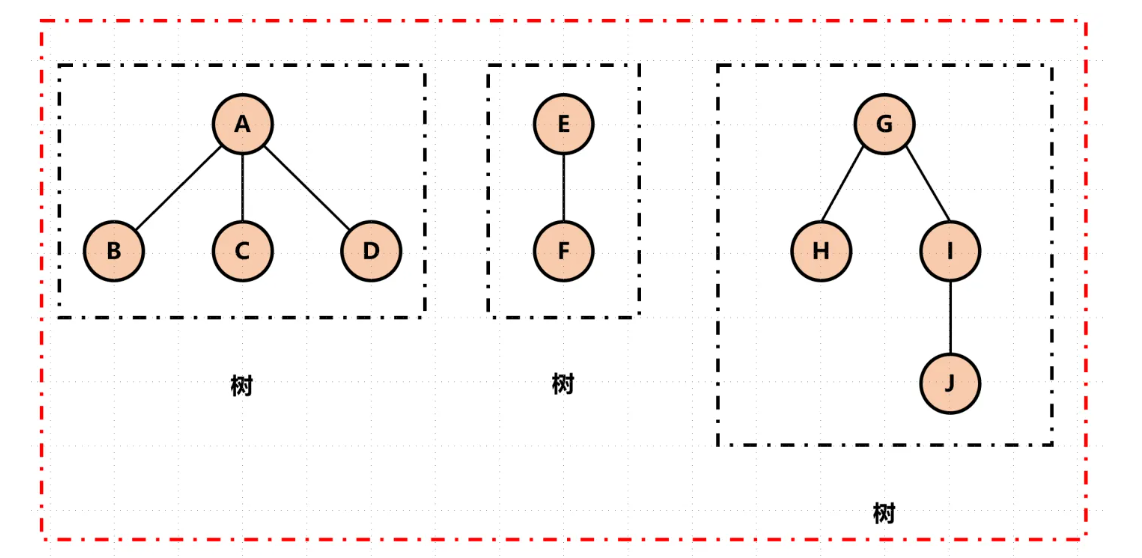

树到二叉树的转化规则是：左孩子右兄弟。每个节点左指针指向第一个孩子，右指针指向他在树中相邻的兄弟。根节点没有兄弟，所以对应的二叉树无右子树。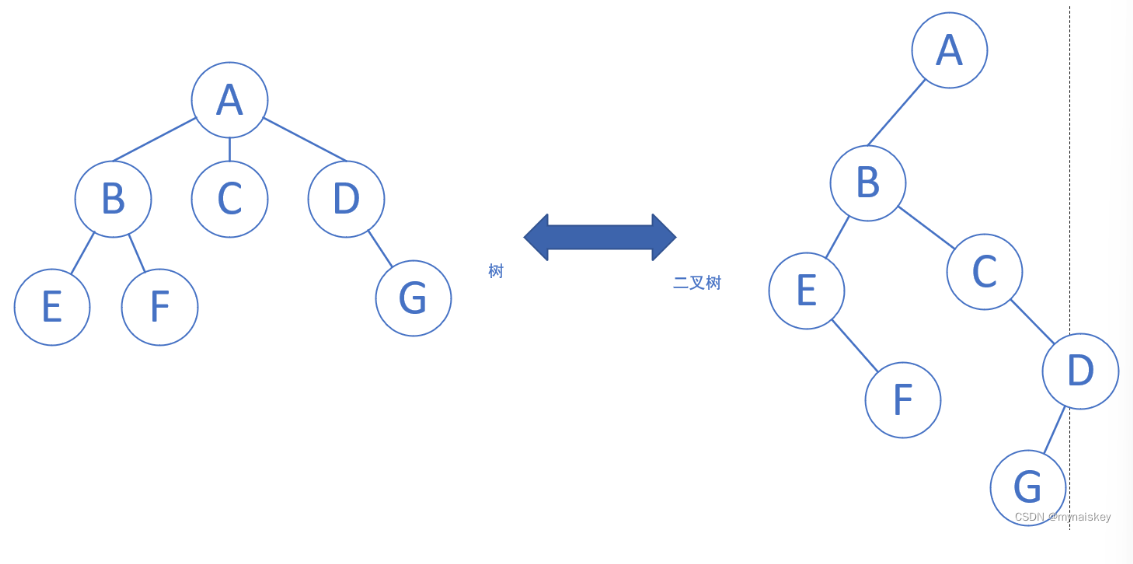

森林到二叉树，先将森林里的每棵树转为二叉树，然后再第一棵树转换的二叉树的右子树接上第二棵树转化的二叉树。

参考：树、森林与二叉树的转换_已知树的结点数怎么求森林的左右子数-CSDN博客