1.datalab-handout

测试命令

make clean//每次更改都要重新编译
make btest//进行测试
./btest -g//以紧凑形式进行测试
./dlc -e bits.c//检测是否符合编码准则

参考

https://blog.csdn.net/FlamelNW/article/details/123039299

int

bitXor

x^y using only ~ and &,用按位运算~和&实现异或。

&是1、1的时候返回1，^是0、1的时候返回1,就拿4和5举例子吧

4：0100 0100 1011 1010 0101 1011

5：0101 0100 1010 1010 0101 1011

x、y是未知的，所以进行~运算的时候一定是对他两个同时。

int bitXor(int x, int y) {
  int z=0;
  int w=0;
  z=x&y;//0100
  x=~x;//1011
  y=~y;//1010
  w=x&y;//1010
  w=~w;//0101
  z=~z;//1011
  z=z&w;//0001
  return z;
}

成功，其实很大程度是连蒙带猜的，毕竟就这两种运算。看看大佬是怎么分析的

思路：用(x&y)定位出共同的1所在，用(x&y)定位出共同的0所在，其余部位就是既有1又有0啦，然后非全0部位和非全1部位进行&运算~~(x&y)&~~(x&y)

tmin

return minimum two’s complement integer，返回补码最小值。

对于一个正数，它的二进制形式就是它的原码，正数的原码补码反码相同。

对于一个负数，反码是将除符号位以外的位全部取反，补码就是将反码加上1。

对于-1

原码：1000 0001

反码：1111 1110

补码：1111 1111

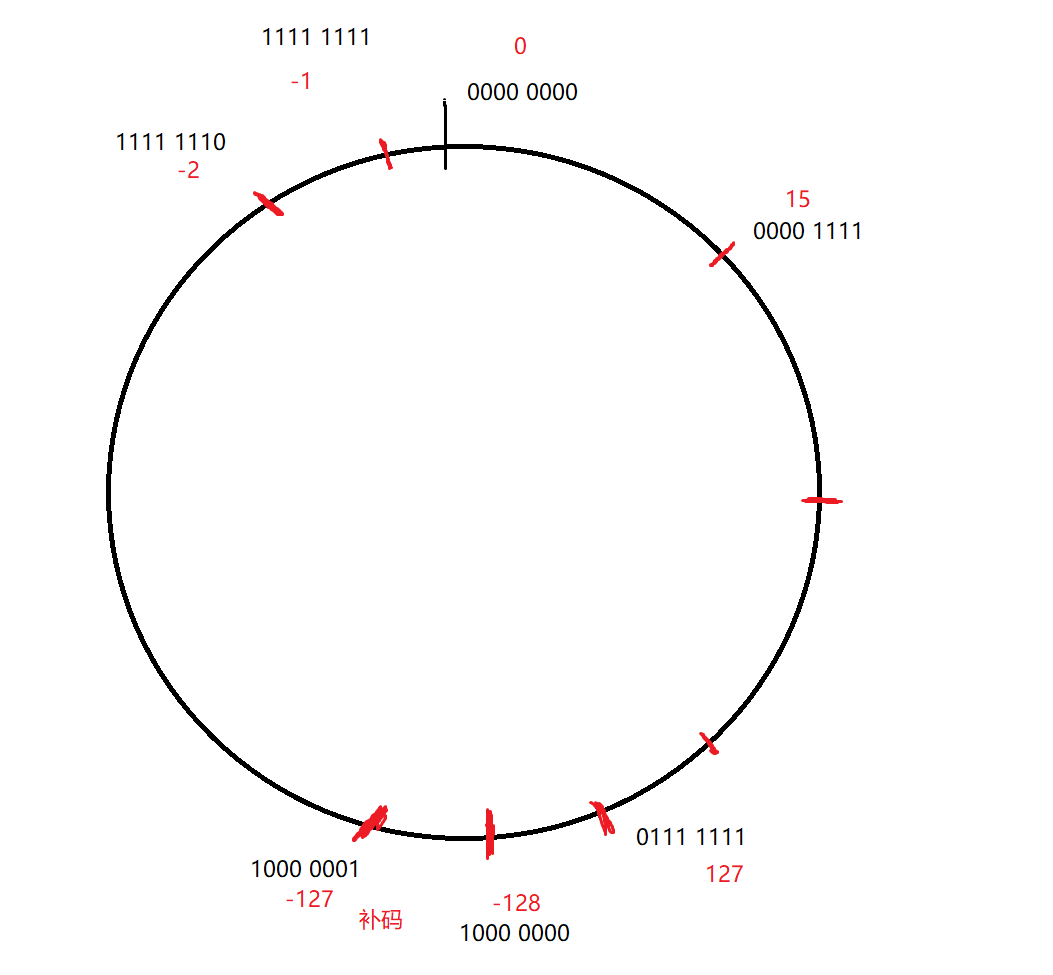
补码最小值，及第32位为1，其余位为0

int tmin(void) {
   int min =1;
   min=min<<31;
  return min;
}

isTmax

returns 1 if x is the maximum, two’s complement number,and 0 otherwise，传来的参数是补码的最大值则返回1，其余情况返回0。

从上图我们可以看到，补码的最大值紧挨着补码的最小值，所以我们只要将最小值减1即可，可是题目不允许使用移位操作符。

经过很长时间的思考，发现根本表示不出最大值，参考了一下，豁然开朗，可以假设传入的参数就是就是最大值。我们可以看出最大值有一个特性，那就是max+1=~~(max+1),也不能完全说是特性吧，因为-1也拥有这个属性，仅此两个。首先我们可以通过max^(~~(max+1)),如果其值返回0那我们可以锁定-1和max这两种情况,接下来我们在排除其是-1这种情况。我们只要找出-1的特性即可，(-1+1)&-1=0,其他的任何数都满足不了这一点。这种做法可以实现函数功能，却没有满足操作符的数量，使用了11个操作符，题目规定不能大于10。参考过后修改一下操作数变成9啦。


int isMax(int x)//如果是max则返回1，其余返回0
{ //int a=((x+1)&~0);//如果x等于-1则返回0，其余的所有数都是非零
  int a=x+1;//这样也能判断是否为-1
  int b=(x^(~(x+1)));//如果是max或—1则返回0，其余的会返回非0
  int c=!!(!a)^(!b);！！可以使非零值返回1
  return c;
}

参考一下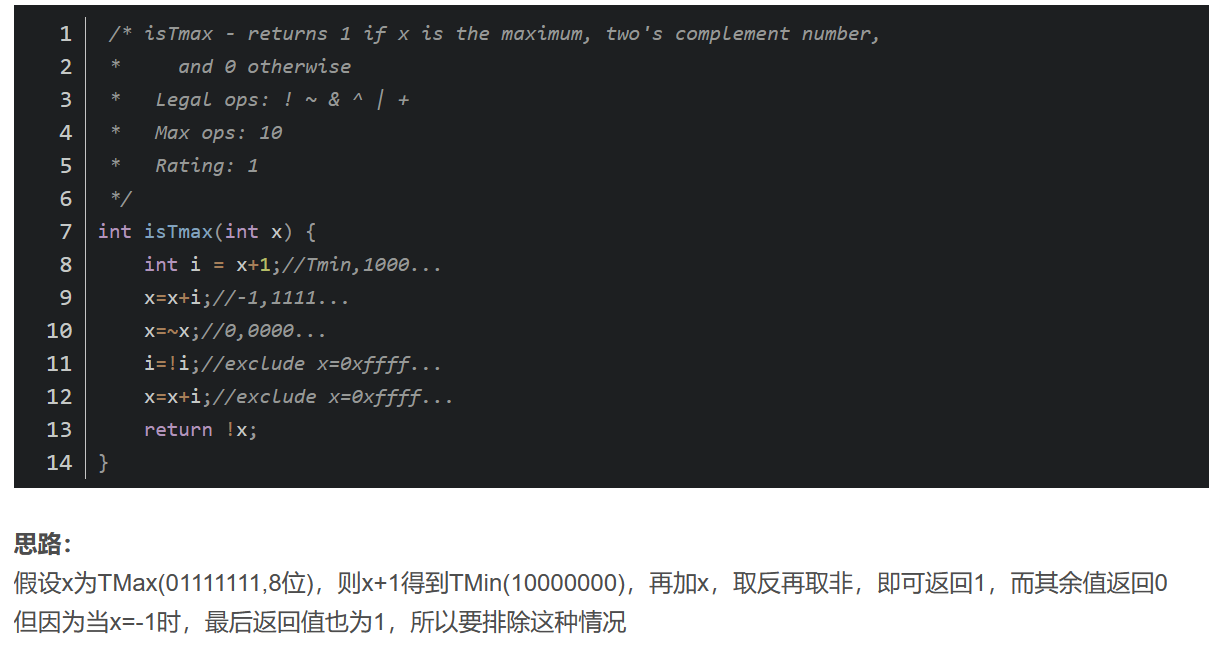

allOddBits

return 1 if all odd-numbered bits in word set to 1，如果所有的奇数位都为1则返回1，最左侧为第31位，最右侧为第0位。

我们可以看看奇数位为1的数有什么共同点。

额，这我只能说是毫无头绪好吧。奇数位必须为1，偶数位不做要求。灵光一现：左移偶数位，得到的数一定是负数。然而并没有什么卵用。直接选择参考。data=1010 1010(32位)，参数x^data,如果x满足要求，则返回data。

//题目要求可以使用的最大的数为0xff即1010 1010 我们要通过移位操作构造出32位奇数位全为1的data
int a=0xAA;//1010 1010
int a2=a<<8|a;//1010 1010 x 2
int data=((a2<<16)|a2);//1010 1010 x 4 32位
int mid=x&data;//x的偶数位全部变成0，奇数位是1则1，是0则0,即如果x奇数位全部为1则返回data
int final=mid^data；//如果x为符合，则mid==data，则异或结果为0
return !final;//final为0则符合，题目让返回1

可以这么说，这题要是不看点提示，想一天也想不来。还是按位操作这里有所欠缺。

negate

return -x ，返回-x。即返回一个数的相反数

这题比较简单，我们直接看一个数和他的相反数在二进制形式上有什么异同点。可以看出，只要按位取反再加上1即可

//0000 0001   1
//1111 1111  -1
//0000 0010   2
//1111 1110  -2
//0111 1111   127
//1000 0001  -127
int negate(int x)
{
  return (~x)+1;
}

isAsciiDigit

return 1 if 0x30 <= x <= 0x39 (ASCII codes for characters ‘0’ to ‘9’)，如果传来的参数是数字则反回1

//Legal ops: ! ~ & ^ | + << >>
//0x30  0011 0000
//0x31  0011 0001
//……
//0x39  0011 1001
int a=(x>>4)^3(0011b);//若a为0，则说明前28位相同，我们只用再判断后四位即可,若不同则返回值非零
int b=(x>>4)^(x+((~10)+1)>>4);//后四位如果是0~9则返回非零，如果不是则返回0
return !(a|(!b));//如果前28位相同，且后四位小于10则返回1

解释一下最后一行，假设x是数字，则a=0，b≠0，c=!b=0，所以a|(!b)=0，反之a|(!b)≠0，所以在前面加上一个！。

conditional

same as x ? y : z 如果x非零则返回y如果x为零则返回z。

int a=!!x;//如果x为零则返回0，如果x非零则返回1
int b=(~a)+1;//如果a=0则返回0(全0)，如果a＝1则返回—1(全1)
return ((b&y)+((~b)&z));//如果x为零则b为零，则返回z，反之返回y
//最后的return 也可以写成这样：return (b&y)|((~b)&z)

isLessOrEqual

if x <= y then return 1, else return 0 如果x<=y,返回1，反之返回0

Legal ops: ! ~ & ^ | + << >>

int a=x+((~y)+1);//a=x-y,如果a<0，则a的最高位为1，如果a>=0,最高位时0，这样有点不好实现，因为小于和等于没在一起
int b=y+((~x)+1);//b=y-x,如果y>=x,则b的最高位为0，反之b的最高位为1
int c=b>>31;//如果成立则返回全0，如果不成立则返回全1
return c+1；

本来以为简简单单大功告成，进行测试发现没分，cao,上面的方法只适合同符号比较。 y>=x等价于y-x>=0在数学是行得通的，可是在计算机中要考虑溢出问题。也就是可能会出现一些比较诡异的情况：

当y<0,x>0时，可能出现y-x>0的情况，比如1000 0000-0000 0001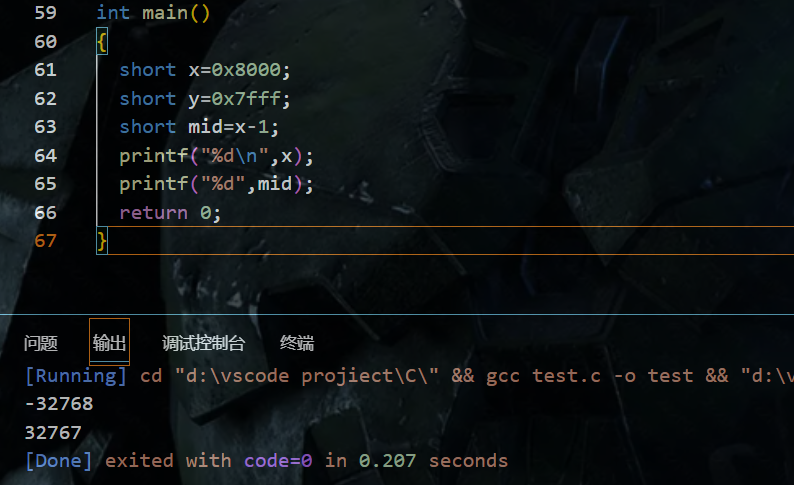

可以看到，由于第一位的1变成了0，所以就变成了正数。

当y>0,x<0时，可能出现y-x<0的情况，比如0000 0001-1000 0000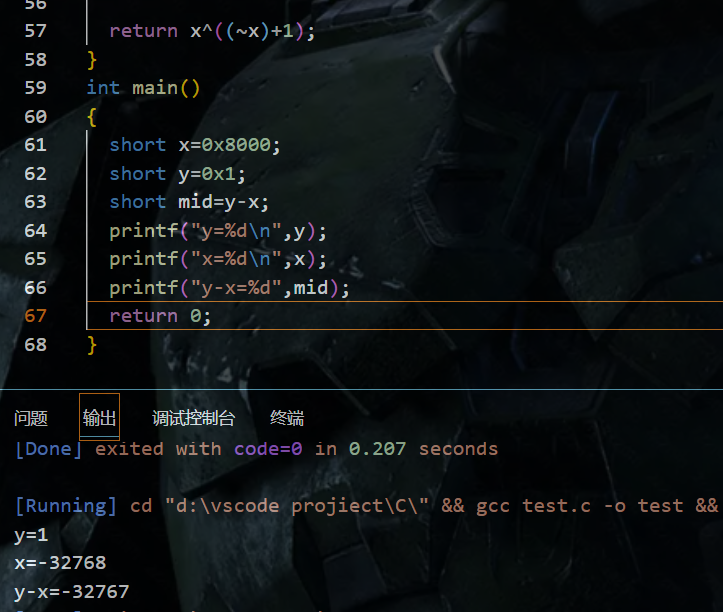

有什么是可以肯定的呢，符号不同时，正数肯定比负数大，符号相同时看差值。

//我测真的烦
int isLessOrEqual(int x,int y)
{
    int singX=(x>>31)&1;//如果不&1，负数情况下就会返回-1
    int signY=(y>>31)&1;
    int signY_X=((y+(~x+1))>>31)&1;//y-x如果大于等于则返回0，小于则返回1
    int checknSign=signX^signY;//相同为0，不同为1
    return (!checkSign&!signY_X)|(checkSign&signX)
}          符号相同，看差的符号         符号不同时，x<0则返回1

这个return比较长，我们分开来看一下其实很简单，

左半部分：!checkSign&!signY_X，符号相等的情况，符号相等不用考虑溢出的问题，我们可以直接根据差值的符号进行大小的判断，符号相等则check为0，signY_X如果满足则为0，否则为1，这里我们倒换一下，也就是满足时返回1，不满足时返回0，如果出现符号不相等，则左半部分返回0

右半部分：如果符号相同则右半部分返回0，如果符号不同，那么我们只需要看x的符号即可，如果x是负数，一定满足条件则返回他的符号1

反思：卡在这里很久很久，因为什么？？？一个很重要的原因对按位运算|掌握得不够熟悉，看到很多师傅的解前面有很多都使用了|，从这一题往后很难不用到|，不能再简单的使用加减。

logicalNeg

implement the ! operator, using all of the legal operators except !

Legal ops: ~ & ^ | + << >>

使用其他合规操作符实现！，也就是传入的参数为0则返回1，非零则返回0

思路零：未完成

int logicalNeg(int x)
{
//0   0000 0000     0的相反数是0 相反数和自身异或取其符号位，为零则为零，非零则为1
//正数 0000 1110
//负数 1000 0100
//0 异或0为0
   int signX=(X>>31)&1;//获取x的符号，负数则为1
   int _signX=((~x+1)>>31)&1;//获取-x的符号
   return signX^_signX^1;
   //零异或上自己的相反数为0，其他数为1，在异或上1，改变符号
} 
int xor0=(0^x)>>31&1;x为零和正数则为0，负数返回1
    //我们需要这样一个数，等于零时返回1，其余时候返回0 死循环

运行失败，看以下错误原因

0x80000也就是最小数10000000这里出现了错误，我们知道对于有符号整型，负数范围比正数大一，所以表示不出来最小数的相反数，这个数和零一样，相反数等于自身。收到一位师傅的启发，我们可以给符号位取反，这样0x80000的符号位就变成0，不造成影响

思路一：

int logicalNeg(int x)
{
   int _x=~x+1;
   int sign=(((~x&~_x))>>31)&1;
    return sign;
   取反后非零数相反数进行&运算符号位为0，如果不进行取反操作则不能绕过0x8000这个存在，它的相反数和自身符号相同都为1
}

思路二：

一个非零数或上自己的相反数其符号位总是1，最小值0x8000也不例外，虽然它的相反数无法表示，但其最高位都是1

int logicalNeg(int x)
{
    int sign=(x|(~x+1))>>31;如果是零则返回0000，非零则返回1111
    return sign+1;
}

都是用到相反数，只是如果使用异或的话不可行，因为0和min的相反数最高位相同，所以只能考虑使用|或&。

howManyBits

return the minimum number of bits required to represent x in two’s complement 返回用二进制补码表示x的最小位数，比如1、0只用一位即可表示

-1也是1，因为-1的补码是1111 1111其实等价于1，补码101和1101代表的都是-3，所以-3最少需要三位，补码的最高位是符号位，就像非负数01和001、0001代表的都是1，前面有多少0都无关紧要，对于负数的补码，前面有多少个1都无关紧要，用数学来解释的话就是最高的两位之和是个定值，对于101最高两位是-2=-2，对于1101最高两位是-4+2=-2。

负数以补码的形式储存，正数的原码补码反码相同。思路：如果是整数那就检索其最高位的1的位置，如果1首先出现在了第三位，比如0101，最高位的1所在的位置就是3，那么这个数最少就可以用3+1位来表示,加的那个1是符号位。对于负数，我们检索其最高位0出现的位置，11101，0出现在第2位，那么最少可以用2+1（符号位）来表示此数，对于-1也就是全1，可以用1表示，仍然符合，也就是它的第0位是0然后我们加上1。

那么怎么检索呢？一个一个来肯定是不能满足操作符数量上的要求的。可以用二分法，我们处理的int是32位的，我们可以先检测它的前十六位，比如说如果全部位0，那么肯定可以用16及更少的位来表示它，再检测其余十六位的前八位，如果不全为零，那么我们继续缩小范围，检测前八位的前四位……

具体怎么实现还是参考的网上的，两个主要操作：计数和缩小范围

int howManyBits(int x) 
{
   int a0,a1,a2,a4,a8,a16;
   int w;//位数
   int sign=x>>31;//如果是正数返回全0，如果是负数返回全1
   x=(~sign&x)|(sign&~x);//如果是非负数则返回x，如果是负数则按位取反
   a16=(!!(x>>16))<<4;//右移16位，两次取非，左移4；如果如果没出现1则高16位为0则返回0，如果出现1则非零则返回16
   x=x>>a16;//如果高十六位非零，右移16位；
   a8=(!!(x>>8))<<3;//如果前十六位为0，则检测其前24位，如果无1，则返回0，如果出现1，则返回8；如果前十六位不为0，则检测32~25位，如果为0则返回0，否则返回8
   x=x>>a8;//如果a8非零则右移8位；
   a4=(!!(x>>4)<<2);//如果前8位为零的话，检测其前28位；如果前8位不为为零的话，这一步检测其前四位（32~29位），如果非零则返回4，为零返回0；
   x=x>>a4;
   a2=!!(x>>2)<<1;//如果24位为零的话，则只检测其前30位，为零则返回0，出现1则返回2；
   x=x>>a2;//如果a2非零则右移四位
   a1=!!(x>>1);//如果前30位为零的话，则检测其前31位。
   x=x>>a1;//如果a1非零则右移两位
   a0=x;//如果前31位为零，那么x要么是1，要么是0
   w=a0+a1+a2+a4+a8+a16+1;
   return w;//1是符号位
   
}

float

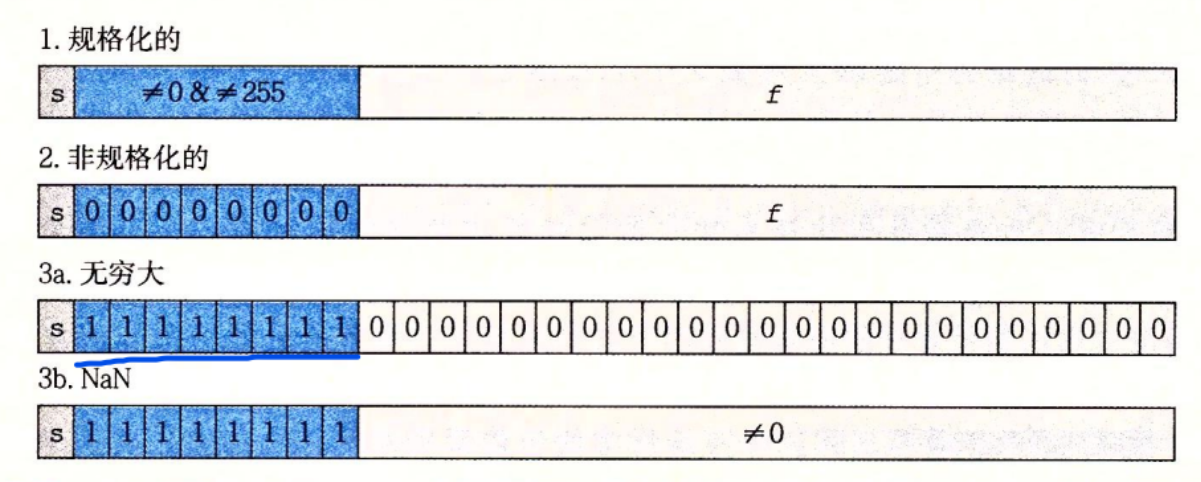
float型符号阶码尾数位分别为 1、8、23，

规格化的，尾数以隐含的1开头，E=e-bias

非规格化的，尾数无隐含的1，E=1-bias

floatScale2

Return bit-level equivalent of expression 2*f for floating point argument f.将传来的参数当成float的位级表示，返回浮点数乘2的位级表示，如果是NAN和极大值(阶码全部为1)则返回0x800000(1000 0000)

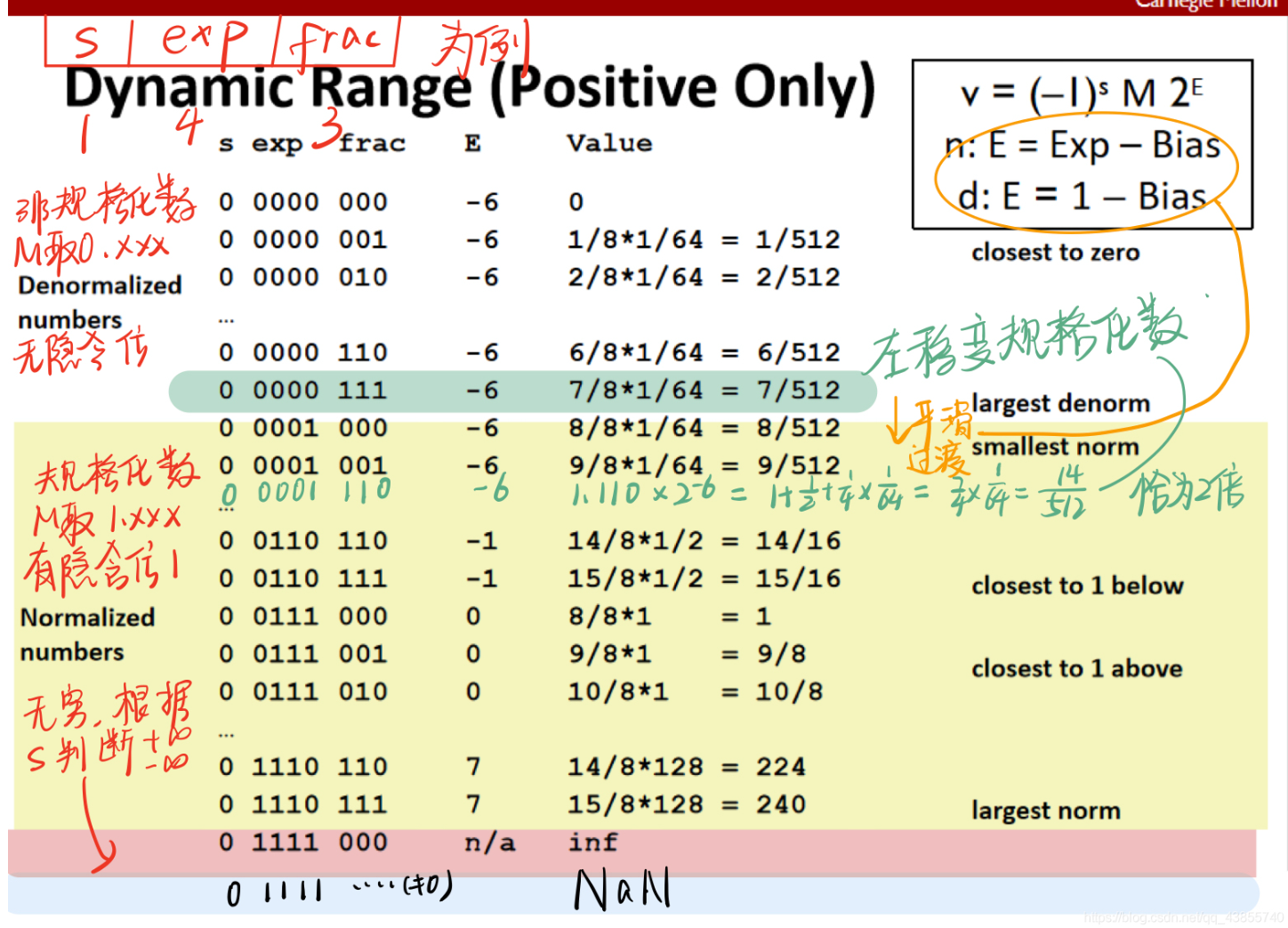
思路：对于规格话数，乘2只需要将阶码+1，其它位保持不变

非规格化的数左移一位即可得到2倍，原因见下图。参考：https://blog.csdn.net/qq_43855740/article/details/106843924

unsigned floatScale2(unsigned uf) {   //拿1来举例子0    0000 0000    0000 0000 0000 0000 0000 001
  unsigned int s=((uf>>31)<<31);//符号            0    0000 0000    0000 0000 0000 0000 0000 000 
  unsigned int e=((uf>>23)<<24>>1);//获得阶码     0    0000 0000    0000 0000 0000 0000 0000 000
  unsigned int m=((uf<<9)>>9);//获得尾数           0    0000 0000    0000 0000 0000 0000 0000 001
  if(e==0)
   return (uf<<1)|s;//非规格化数左移1位变为两倍，再恢复其符号位
  if(e==0x7f800000)//无穷大和非规格化数 无穷大的二倍还是无穷大
   return uf;
  e=(((uf>>23)+1)<<24>>1);//获得阶码+1 
  unsigned int r=s+e+m;
  return r;                     
}

floatFloat2Int

Return bit-level equivalent of expression (int) f for floating point argument f.将浮点型转换为位级等价整数 Anything out of range (including NaN and infinity) should return 0x80000000u.

取出他的符号指数和尾数。

int floatFloat2Int(unsigned uf) {
    int s=uf>>31&1;//取符号
     int e=(uf<<1>>24)-127;//e属于(-127~126)
     int m=uf<<9>>9;//尾数
     m=m+0x800000;
     int r=0x80000000;
    if(e<0)//小数点左移，实际的数就是0.xxx
        return 0;
    if(e>31)//溢出，包括NaN
        return r;
    if(e>23)
        m=(m<<(e-23));
    else
        m=(m>>(23-e));
    int mSign=m>>31&1;
    if(s)//如果传来的参数是负数，那么我们直接将得到的数取反
      return -m;
    else//传参为正数
      return m;
}

floatPower2

Return bit-level equivalent of the expression 2.0^x (2.0 raised to the power x) for any 32-bit integer x.以浮点数形式返回2^x=r

2的多少次方，其尾数全零，隐含1，我们只需要将e改为127+x即可

unsigned floatPower2(int x) {
    int e=x+127;
    if(e<0)
        return 0;
    if(e>=255) 
        return 0x7F000000u;//返回+INF（正无穷大）
    else
        return (e<<23)|0;
       
}

完结撒花

fishjump's blog

csapp.lab