前言
记录一些自己的看法和心得。
第一章 计算机系统漫游
不知道是个人的原因,还是此章节比较特殊的原因,读了一遍,感觉没有进脑子什么东西。查看了一些笔记,说是有一定的C语言基础即可阅读,而第一章更是给读者们找自信的一个章节,这使我十分的迷茫。遇到困难我们就要勇敢的面对困难,硬着头皮整理一下吧。
信息就是位+上下文
0和1组成位,也成为比特,八个位组成一组称为字节。系统之中所有的信息都是由一串比特表示的,区分不同数据对象的唯一方法就是对照上下文。举个简单的例子,0110 0100,这么一串比特,它既能表示二进制数,又能表示ASCII对应的值d,具体表示什么要联系上下文。
了解编译系统如何工作的益处(书上这么写的不是我总结的)
1.优化程序性能
2.理解链接时出现的错误
3.避免安全漏洞
了解shell
第一章中不停的在提及shell。shell是一个命令解释器,他输出一个提示符,等待输入一个命令符,然后执行这个命令。简单的理解一下,Windows系统中我们打开一个程序需要点击其图像,Linux则需要我们输入命令行来打开,shell就是那个供用户输入命令行的程序。shell是一个应用程序,连接了用户和linux内核。参考:(http://c.biancheng.net/view/706.html)
系统是硬件和软件互相交织的集合体(简单介绍一下硬件)
1.总线
像神经一样,贯穿于整个系统,携带信息字节并负责在各个部门传递
2.I/O设备
及输入/输出设备,键盘、鼠标为输入设备,显示器和磁盘为输出设备。
3.主存
主存是一个临时存储设备,在处理器执行程序时,用来存放程序和程序处理的数据。
4.处理器
中央处理单元(CPU),简称处理器,世界是(或执行)存储在主存中指令的引擎。处理器的核心是一个大小为一个字的存储设备(或寄存器),称为程序计数器(PC)。在任何时刻,PC都指向主存中的某条机器语言指令(即含有该指令的地址)。
不大不小的疑惑
此时年轻懵懂的我不明白为什么有很多很多人念着Linux系统的好,Windows这种图形化控着与此相比有什么难以弥补的劣势?据说以后工作实践中,项目大多也是基于Linux完成的,有时间了一定好好了解一下其中的内幕。
第二章 信息的表示和处理
研究数字的实际表示的意义
能够了解可以表时得知和不同算术运算的属性。从而使程序正确工作,更具可移植性,更安全。

信息存储
大多数计算机使用8位的块(字节)作为最小的可寻址的内存单元。机器级的程序将内存视为一个非常大的字节数组,称为虚拟内存。内存的每个字节都由一个唯一的数字来标识,称为它的地址。所有可能地址的集合称为虚拟地址空间。
十六进制表示法
二进制表示起来过用冗长,而十进制与二进制的转化很麻烦,十六进制表示起来很方便。如果二进制位数不是4的倍数,最左侧补0。

j代表的是16进制0的数量。前面的i是1的数量,注意只能是1,11,111,1111这四种表示。

整型
字数据大小
字长决定虚拟地址空间的最大大小,我们常说的32位64位都是指的字长,32位字长虚拟地址空间为2的32次方及4GB。
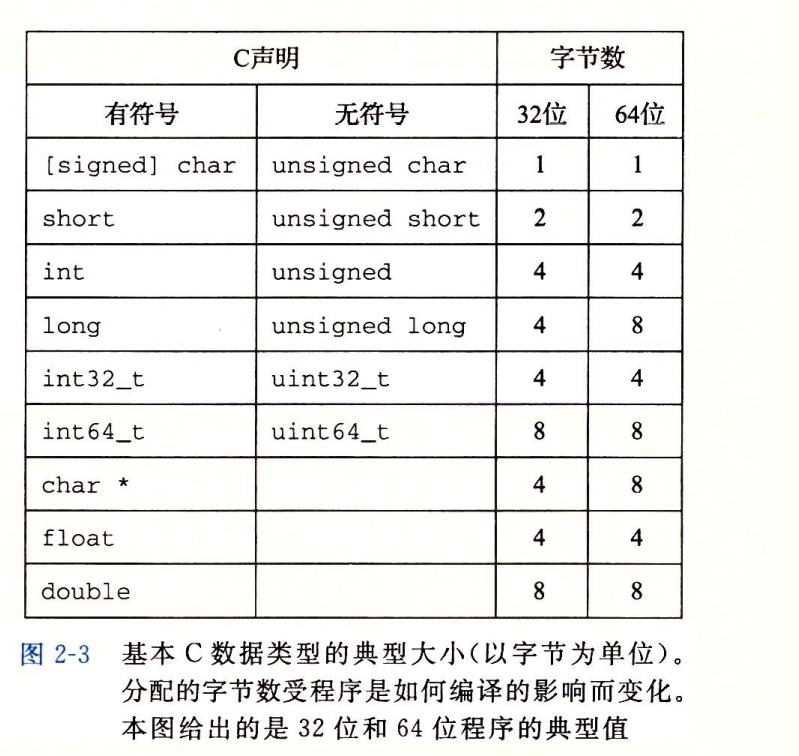

#include<stdint.h>中有关于int32_t等的宏定义,确定的大小可以避免很多麻烦,程序的可移植性也更高。
寻址和字节顺序
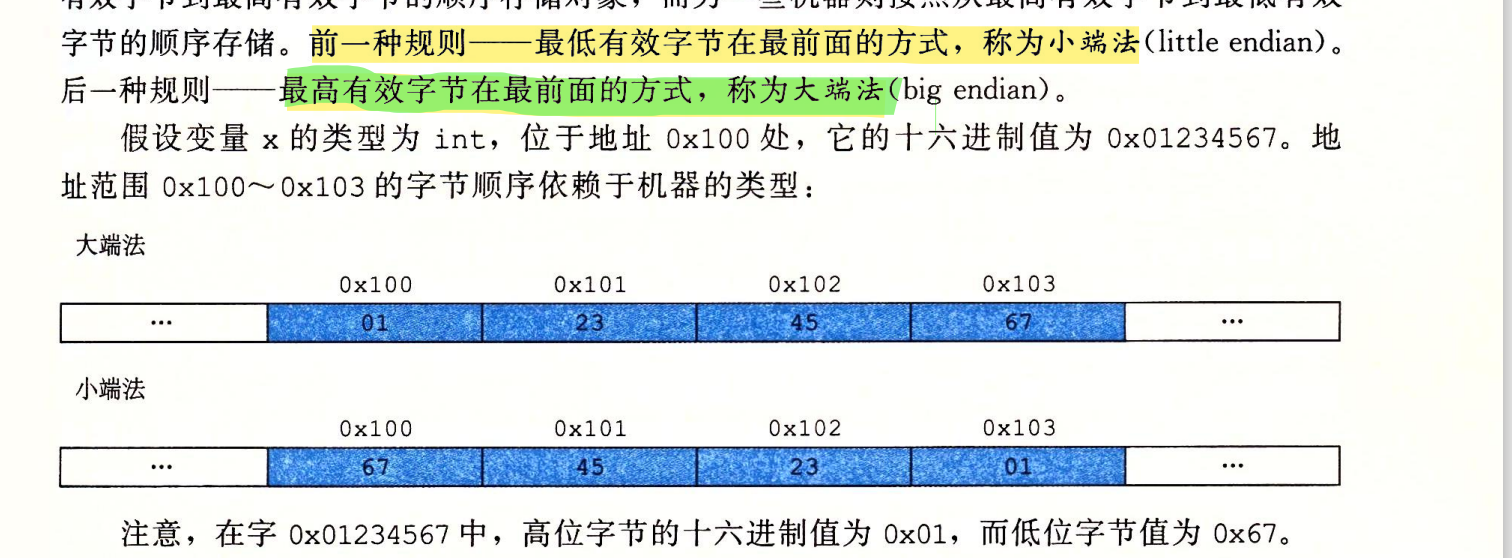
可以这样说,大端是更符合我们日常思维的那一种。两种端序没有优劣之分,选择哪种字节顺序没有技术上的理由。我们只需选择一种并且始终如一地坚持。
C语言中的逻辑运算
逻辑运算和按位运算有很大的不同,其一逻辑运算中所有的非零参数都表示TRUE,0参表FALSE,其二,如果对第一个参数求值就能确定表达式的结果,那么逻辑运算就不会对第二个参数求值。
C语言中的移位运算

几乎所有的编译器都对有符号数使用算数右移(保留最高位),对于无符号数,右移必须是逻辑的。Java中x>>>k是逻辑右移,x>>k是算数右移。

强制类型转换
强制类型转换结果保持位不变,改变的是对位的解析方式
有符号和无符号处理
当表达式中同时出现也有符号和无符号,那么C语言会隐式的将有符号数转换为无符号数(位不变),例如表达式-1<0u返回的结果是0,也就是表达式错误,因为将-1的补码按照无符号数来解析。

看着好像没什么问题,但是当len等于0,在运算0-1时,计算机会当作0+(-1),因为默认是有符号,而len是无符号的。所以(-1)要从补码转换成无符号数也就是T2U,也就是UMax,所以程序会进入死循环,并且访问到a的非法元素。

A.当s比t短的时候会错误的返回1
B.两数相减得到负数会当作无符号数处理,最高位为1也就是一个很大的数大于零
C.改为return strlen(s)>strlen(t)
扩展一个数字的位表示
如果想扩展一个数字,只需要在它的最高位补上n个符号位,比如说101表示-3,在最左侧加1变为1101还是表示-3,我们可以看到它最高位与后一位的和-8+4=-4这也是扩展前符号位的值,我们再给它扩展一位变为11101它还是表示-3,对于非负数我们只需在其前面补上0即可,正好今天在做datalab的howManyBits,和这个正好是相关的,刚开始看到网上师傅举得例子还有点懵,为啥101和1101代表的都是-3,所以我们可以知道有无数种形式的补码可以表示-3,而101是最短的一种。
截断数字
截断无符号数:

对于整数运算最后的思考 模运算
计算机执行整数运算实际上是一种模运算,什么是模运算呢?模运算也就是求余运算,在前面我们可以看到几乎所有的溢出都采取了模最高位取余数的方法。补码的表示,可以使正数加上负数的补码等于减去其原码比如
1 | 3-2 |
浮点数
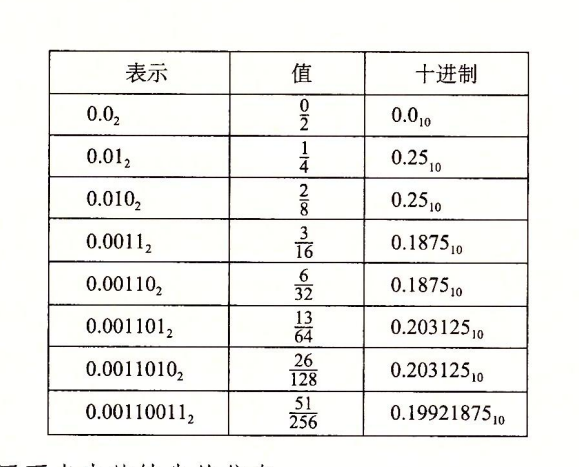
二进制小数
二进制小数,小数点左边是二的非负权(非负幂),小数点右边是二的负权,这一点和十进制小数并无区别。
二进制小数只能精确的表示形如(x*2的y次幂)的数
IEEE浮点数表示
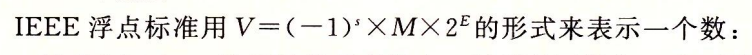

正如书中提到的,浮点数看起来比较深奥难懂,但它是建立在小而一致的原则之上的。
根据exp的值,可以分为三种不同的情况,规格化的、非规格化的或特殊值
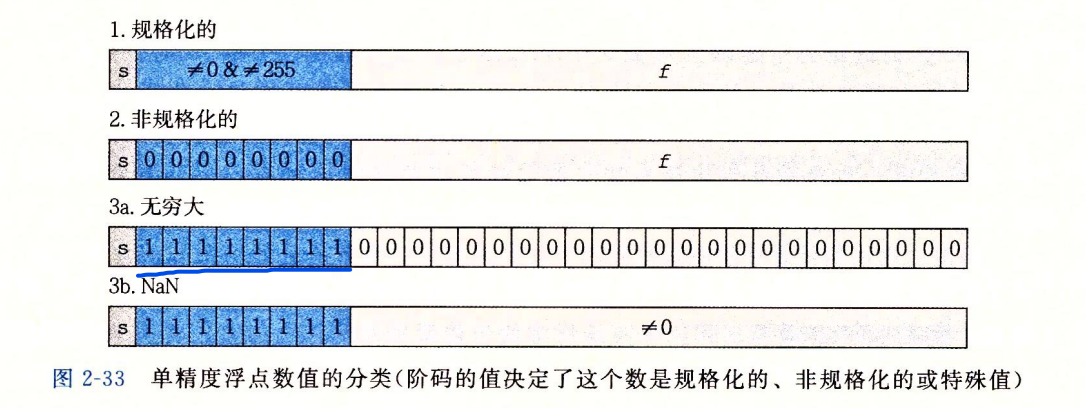
规格化得值

小数点在f段最高位的左侧,隐含的以1开头表示。
偏置值
这个师傅讲的比较简单明了:
拿单精度来说,(规格化)e的取值范围是0000 00011111 1110也就是1254,肯定不能只使用无符号表示,因为这样只能表示非负数,所以使用E=e-Bias,其范围就是-126127,那么为什么不直接用补码表示e呢?这样E的范围就是1111 11110111 1111=(-128~127),可以看出使用偏置和使用补码表示的范围相差不大,还可以不用考虑符号

非规格化的值

特殊值

舍入
浮点数浮点数采用向偶数最接近的偶数舍入的方法,这样对与那些处在中间的数在50%的时间里会向上舍入(1.5—>2),在另外的50%的时间会向下舍入(2.5—>2)。
浮点数运算


下面是对3丢失的解释,所以说浮点数计算不符合结合律
1 | 对于float 符号位 阶码 尾数分别为 1 8 23 |
第三章 程序的机器级表示
数据格式
从十六位过渡到64位不显得突兀,在指令后面加了字符后缀,确定大小
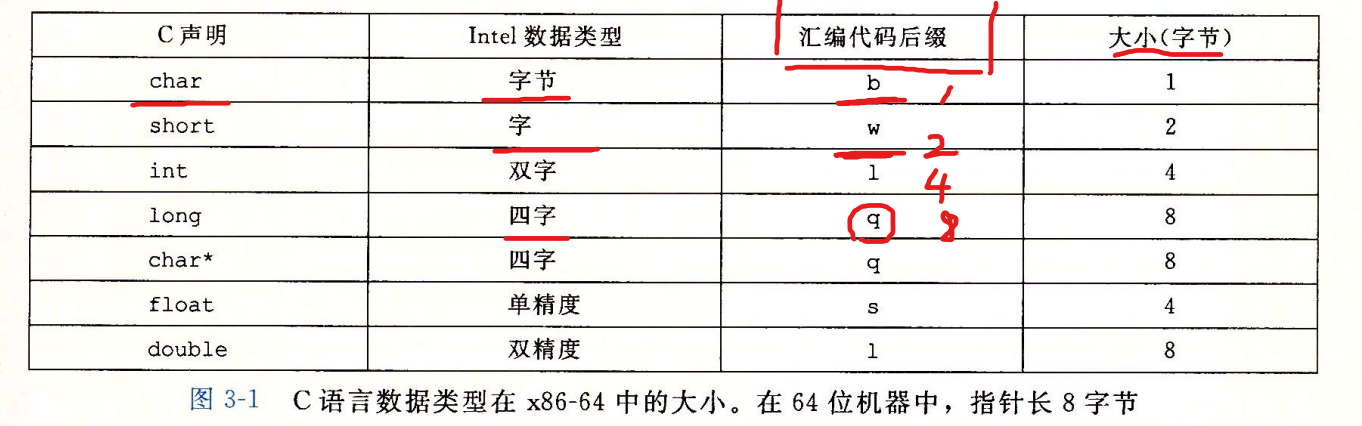
访问信息
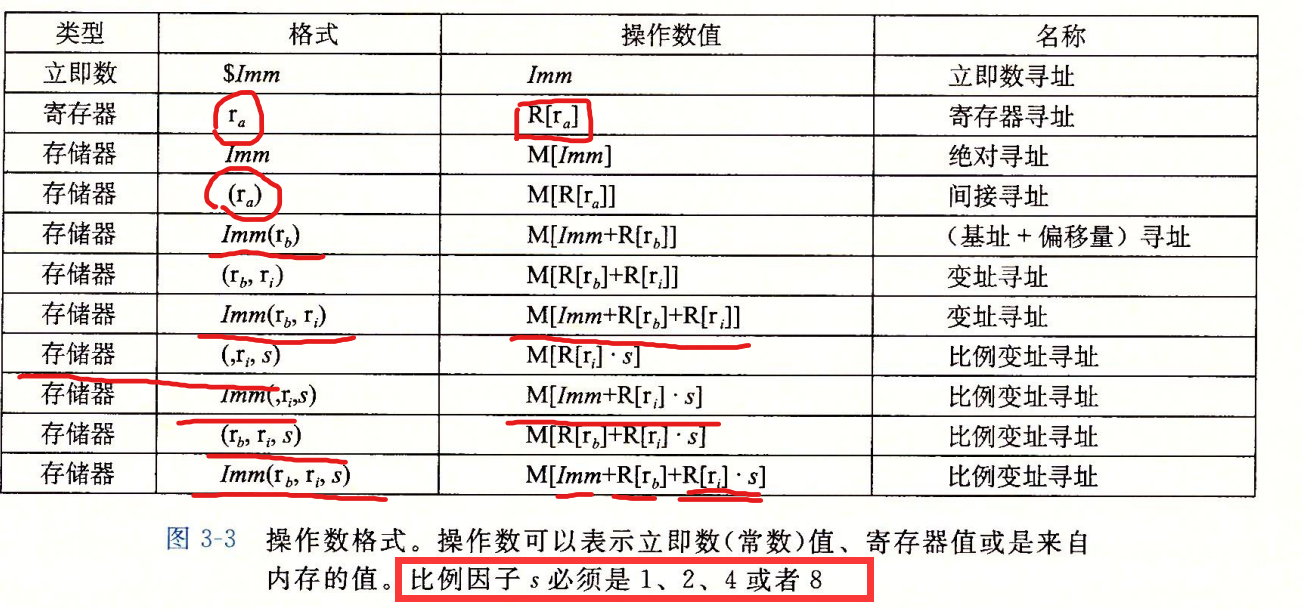
ATT和Intel

之前接触的是intel的导致我以为这里出现了错误
栈
更新一点对栈的认知,之前一直以为将栈顶的值pop之后,内存中的值会消失,原来值会一直存在,直到被覆盖。
算术和逻辑操作
算术操作
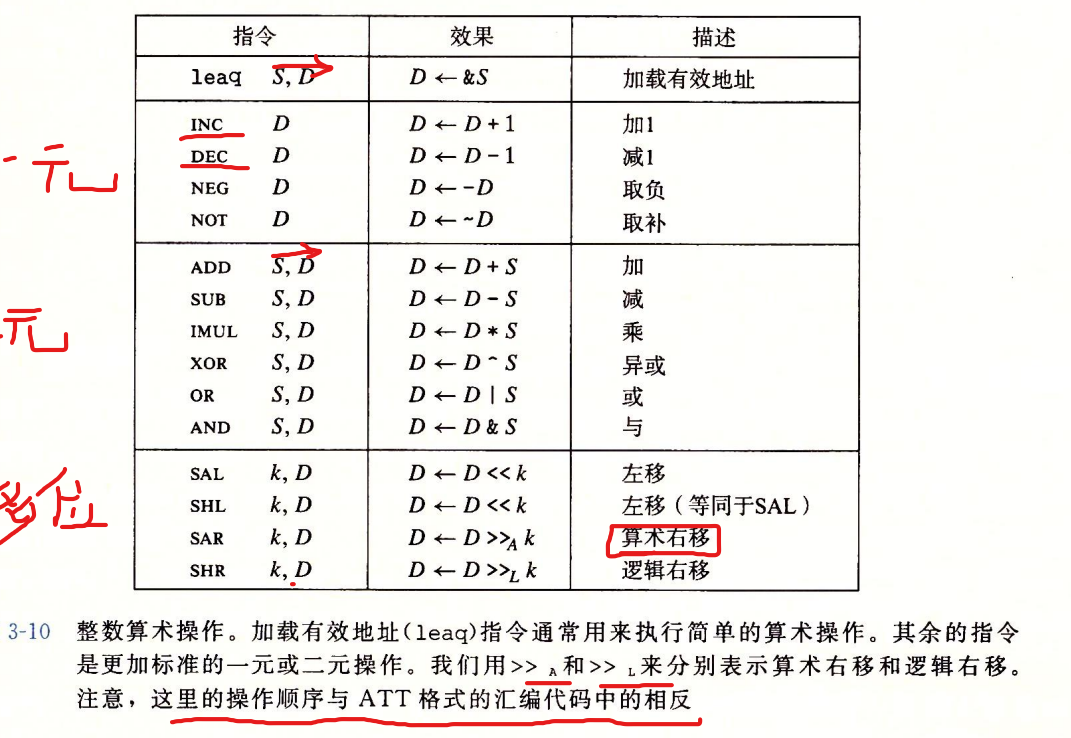
条件码

函数传参和寄存器的关系

是按照这个顺序进行传参,并且返回值默认是ax。